7y−2x=−3(1) 4y3x=19(2) Let us use the elimination method to solve the given system of equation Multiply (1) by 3 and (2) by 2 And add both the equations Adding 29y=29⇒y= 29 29 =1 21y−6x=−98y6x=38 Substitute the value of x in equation (1), we have 7(1)−2x=−3 x=5 Answer x=5 and y=1 Misc 16 Solve the system of the following equations 2/x 3/y 10/z = 4 4/x 6/y 5/z = 1 6/x 9/y /z = 2 The system of equations are 2/x 3/y 10/z = 4 4/xSolve by the method of elimination (i) 2x – y = 3;

Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3
2^x 3^y=17 2^x 2-3^y 1=5 by elimination method
2^x 3^y=17 2^x 2-3^y 1=5 by elimination method- Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓 Hence, x = 19/5,𝑦=6/5 Ex 34, 1 Answer x=3 y=2 2^x = p 3^y = q p q = 17 1 (2^x X 2^2) (3^y X 3^1) = 5 Substitute values of 2^x and 3^y 4p 3q = 5 2 Solve equations 1 and 2 p = 8 2^x = 8 x = 3 Similarly, y = 2




Blogjpmbahebyvn コンプリート 2 X 3 Y 17 2 X 2 3 Y 1 5 50
Online math solver with free step by step solutions to algebra, calculus, and other math problems Get help on the web or with our math appQuestion 4841 Solve the system by the addition method x/3y/2=5/6 x/5y/3=3/5 Answer by rapaljer(4671) (Show Source) You can put this solution on YOUR website! Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13 – 3V u = (13 − 3𝑣)/2
Transcript Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our equations are 5u v = 2 (3) 6u – 3v = 1 (4) From (3) 5u v = 2 v = 2 ab = 17 4a 3b = 5 first one by 3 3a 3b = 51 4a 3b = 5 a = 46 b = 63 then 2^x = 46 , which is not possible in the real number set So for 2^x 3^y = 17 to be true, we would have add a "nonexisting number" to 3^y to get 17Algebra Solve by Addition/Elimination 2xy=3 3xy=17 2x y = −3 2 x y = 3 3x − y = −17 3 x y = 17 Add the two equations together to eliminate y y from the system 2 2
Y = 2/2 = 1 Hence, solution of the given system of equation is x = 1, y = 1 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution MethodGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! x=1 y=2 You must make an equation that has only one variable in it so you can solve for that variable By finding the variable you can use it to find the other one Let's solve for y xy=3>y=3x substitute (3x) instead of y in x=3y5" " we get x=3(3x)5 x=93x5 4x=4 "x=1" Now we need to find y, we know that xy=3, and we know that x=1, so we substitute 1 instead of x xy=3>1y=3 "y=2"




Solving Linear Systems By Elimination
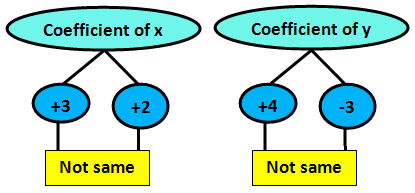



Elimination Method
L w 12 5 Answers may vary For example 005n 010d 070; x = 5 Insert this value into the first or second equation, whichever For example 3 x y = 17 3 ∙ 5 y = 17 15 y = 17 Subtract 15 to both sides y = 2 The solution is x = 5 , y = 22/3x3/5y=17 1/2x1/3y=1 Rewrite each equation by multiplying the LCD of each equation respectively 10x 9y = 255 3x 2y = 6 Use elimination method to solve this system Hint the answer is x = 12 and y = 15 There you go!



Solving Systems Of Equations
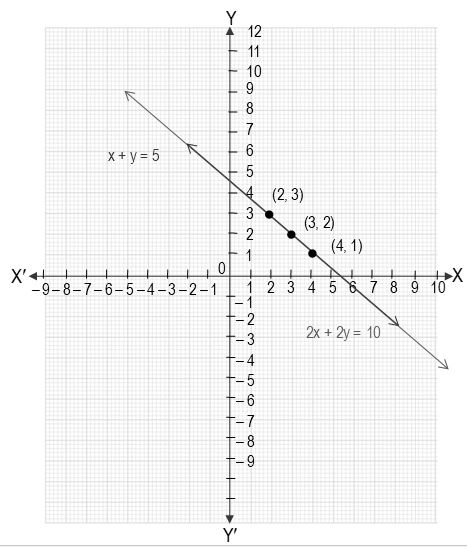



Pair Of Linear Equations In Two Variables
Click here👆to get an answer to your question ️ Solve the following system of equations by using Matrix inversion method 2x y 3z = 9,x y z = 6,x y z = 2Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first




Solve By Elimination Method 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Graph Graph Inequalities With Step By Step Math Problem Solver
X2yz=0, 2xyz=1, 3xy2z=5 \square!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! Just by inspection, and assuming integers, 2^3 3^2 = = 17 But if you want to go through the algebra, using the fact that 2^2=4 and 3^1=3, we have 2^x 3^y = 17 4*2^x 3*3^y = 5 Now, if you let u=2^x and v=3^y, we have u v = 17 4u 3v = 5 and again we have u=8, v=9 so, what are x and y?




7x 3y 1 0




Exercise 2 1 Solutions Studocu
Solve by Addition/Elimination 2x^2y^2=17 , 3x^22y^2=6 2x2 y2 = 17 2 x 2 y 2 = 17 , 3x2 − 2y2 = −6 3 x 2 2 y 2 = 6 This system of equations cannot be solved using the addition method, but can be solved using substitution Can't be solved with addition methodAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}yxy^ {2}=13 x 2 y x y 2 = 1 3 Subtract 13 from both sides of the equationOr click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In
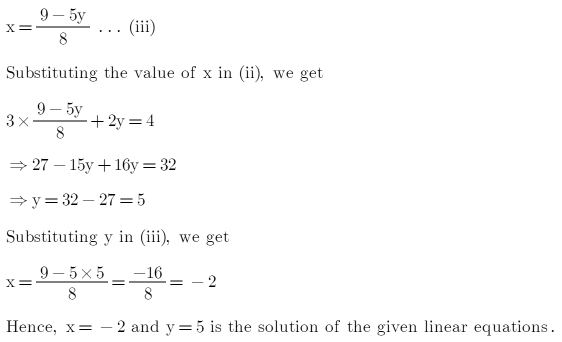



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll
Elimination method x2y=2x5, xy=3 \square! 2xy10=0(1) xy—4=0(2) Adding equation (1) and equation (2),we get 3x—14=0 3x=14 x=14/3 Plug x=14/3 in equation (2) 14/3—y—4=0 14/3–4=y (14–12)/3=y y=2/3Find stepbystep Algebra 2 solutions and your answer to the following textbook question Solve the system using the elimination method 2xyz=9 x6y2z=17 5x7yz=4




Olve By Elimination Method 2power X 3 Power Y 17 2 Power X 2 3 Power Y 1 5 Maths Polynomials Meritnation Com




2 Use Cramer S Rule To Solve The Following Set Of Chegg Com
5n 10d 70 6 The systems are equivalent because equation is equation divided by 3, and equation is equation x multiplied by 2Click here👆to get an answer to your question ️ Solve following equation by elimination method 3x 2y = 11 2x 3y = 4 Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables 3 x 2 y = 1 1, (1) On multiplying by 3, we get 9 x 6 y = 3 3 Solve a System of Equations by Elimination The Elimination Method is based on the Addition Property of Equality The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality
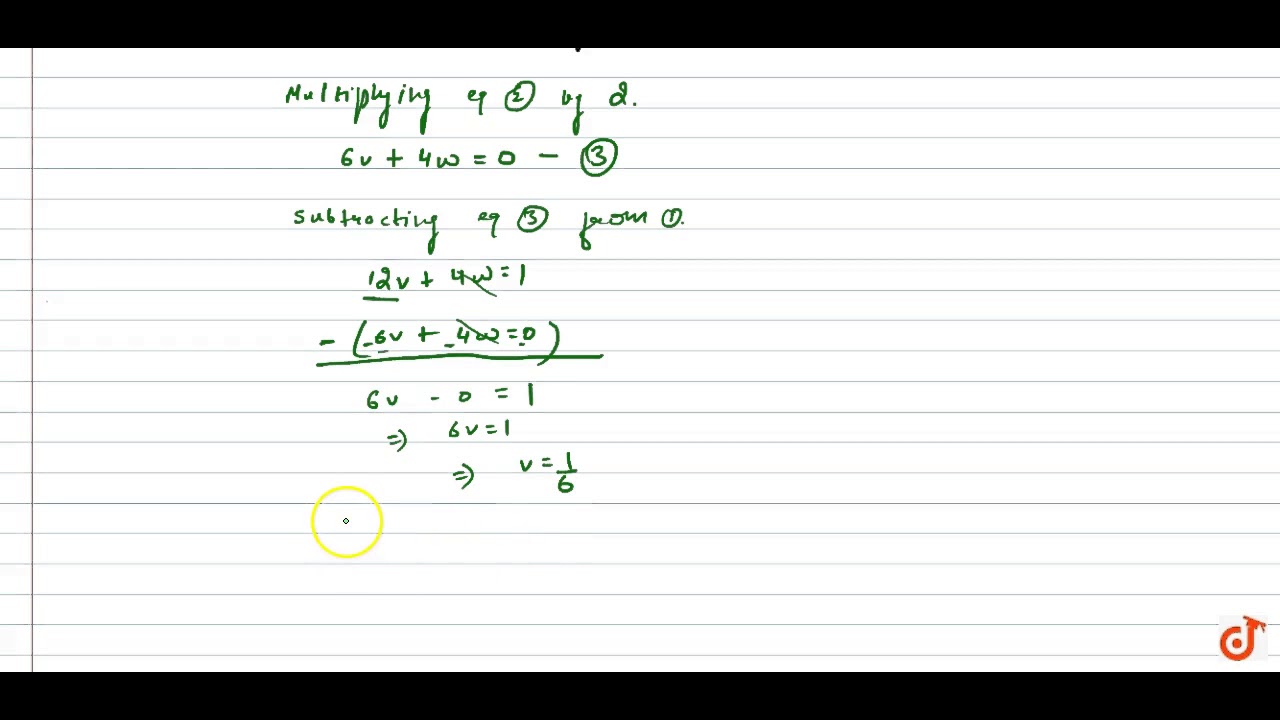



Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For Which Y A X 4 Youtube



1
Solve each system by elimination 1) −4 x − 2y = −12 4x 8y = −24 (6, −6) 2) 4x 8y = −4x 2y = −30 (7, −1) 3) x − y = 11 2x y = 19 (10 , −1) 4) −6x 5y = 1 6x 4y = −10 (−1, −1) 5) −2x − 9y = −25 −4x − 9y = −23 (−1, 3) 6) 8x y = −16 −3x y = −5 (−1, −8) 7) −6x 6y = 6 −6xSolve this linear system using the elimination method 3x – y = 3 x y = 17 Good heavens, the y's are already lined up and signed up for us to eliminate them (3x x) (y y) = (3 17) 4x = x = 5 Plug x = 5 into the second original equation and solve for y 5 y = 17 y = 12 The solution seems to be (5, 12) Let's make a quick check for body doubles, evil clones, or demonicWeekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled




Solve The Equation To Find The Value Of X And Y Using Elimination Method Q 2x 3y 172x 2 3y 1 5 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solving A System Of Equations Using A Matrix Precalculus Socratic
`= x = 42/3 = 14` Hence, the solution of thee given system of equations is x = 14, y = 9 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution MethodClick here👆to get an answer to your question ️ Solve the system of equations 2x 3y = 17, 3x 2y = 6 by the method of cross multiplication Join / Login > 10th > Maths Solve the system of equations 2 x 3 y = 1 7, 3 x Solve the following pair of linear equation by cross multiplication method x 4 y 9 = 0 5 x − 1 = 3 yQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions




Exercise 1 2 Cramer S Rule Problem Questions With Answer Solution




Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver
X y = G What can QuickMath do?Answers • MHR 507 4 Answers may vary For example 2l 2w 24; Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2




Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples
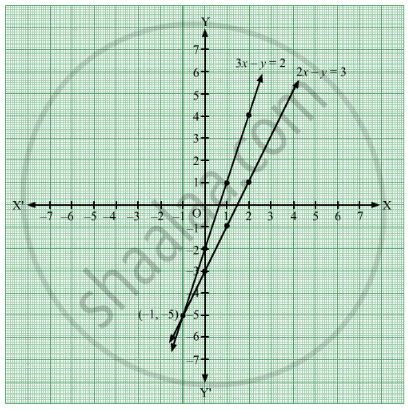



Solve The Following Simultaneous Equations Graphically 3x Y 2 2x Y 3 Algebra Shaalaa Com
Chapter 1 Rational and Irrational Numbers Chapter 2 Compound Interest (Without using formula) Chapter 3 Compound Interest (Using Formula) Chapter 4 Expansions (Including Substitution) Chapter 5 Factorisation Chapter 6 Simultaneous (Linear) Equations (Including Problems) Chapter 7 Indices (Exponents) Chapter 8 Logarithms Chapter 9 Triangles Congruency in TrianglesSolve the given inequalities 3x y ≥ 12, x y ≥ 9, x ≥ 0, y ≥ 0graphically in two – dimensional plane asked Jul 22 in Linear Equations by KumarArun (Let's start by clearing those fractions The LCD for the first equation is 6, for the second equation is 15, so multiply both sides of these equations by those numbers respectively




Exercise 1 2 Cramer S Rule Problem Questions With Answer Solution




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
Solve the following pair of linear equations by suitable method x y = 5 and 2x 3y = 4 Medium View solution Solve the following pairs of linear (simultaneous) equation by the method of elimination 2 x 3 y = 8,Solve the Given equation in Elimination method and Substitution MethodStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2x3y=1;y=x1 Tiger Algebra Solver




Solve For X And Y 4x 3y 1 And 5x 7y 2 By The Method Of Maths Pair Of Linear Equations In Two Variables Meritnation Com



Systems Of Linear Equations Gaussian Elimination Studypug
Solve the equations using elimination method 3 x 2 y = 7 and 4 x − 3 y = − 2 A (1, 1) B (1, 1) C (1, 2) D (1, 2) Medium Open in App Solution Verified by Toppr Correct option is D (1, 2) 3 x 2 y = 7 (1) 4 x3x y = 7 Solution 2x – y = 3 (1) 3x y = 7 (2) The coefficient of y in the 1st and 2nd equation are same (1) (2) 2x – y = 3 3x y = 7 5x = 10 x = 10/5 = 2 By applying the value of x in (1), we get 2(2) y = 3 4 y = 3 y = 4 3 y = 1Free simplify calculator simplify algebraic expressions stepbystep




Solve The Simultaneous Equations X 2y 1 3x Y 17 Brainly In



How To Solve Using The Elimination Method 2x Y 8 3x Y 17 Quora
Introduction The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system \(\ xy=6\) and \(\ xy=8\), you can add \(\ xy\) to the left side of the first equation and add 8 to the right side of the equation ⇒ x = 1 Substituting x = 1 in (v), we get 3 2y = 5 ⇒ y = 1 Hence, x = 1 and y =1 Solve the system of equations by using the method of cross multiplication 1/x 1/y = 7 2/x 3/y = 17 (x≠0 and y≠ 0) asked in Linear Equations by Vevek01 ( 472k points) linear equations in two variables



Solve The Following Systems Of Equations 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Sarthaks Econnect Largest Online Education Community




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In



4 1 Solve Systems Of Linear Equations With Two Variables Mathematics Libretexts




Show That The System Of Equations 2x 5y 17 5x 3y 14 Has A Unique Solution Find The Solution




Solving A System Of Equations Using A Matrix Precalculus Socratic




Solving Linear Systems By Elimination
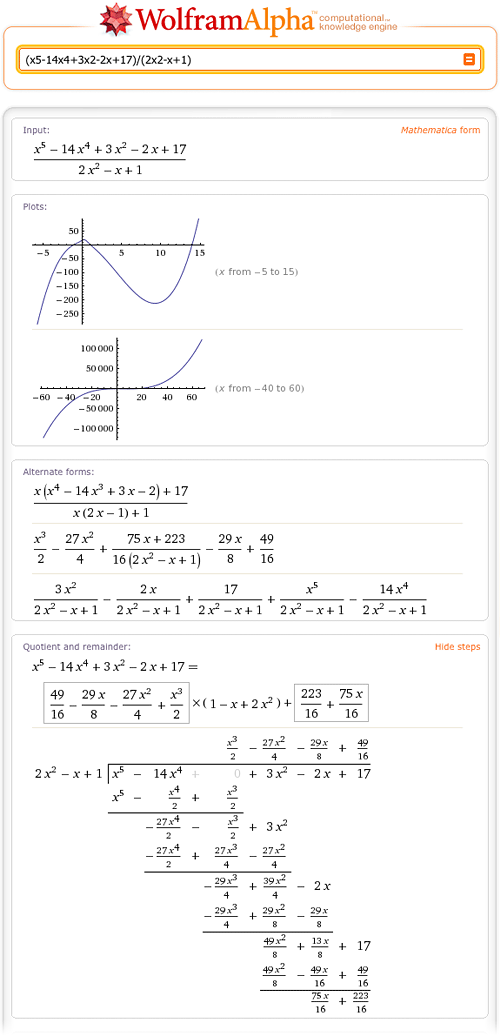



Step By Step Math Wolfram Alpha Blog




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




System Of Equations And Elimination Section 4 3 Overview Solving By The Elimination Method Problem Solving Ppt Download
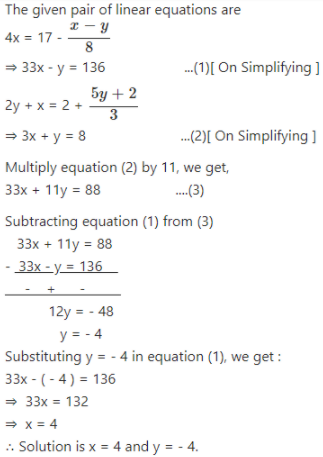



Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solve The Following System Using Gauss Elimination Method X 8y Z 5 X 2y 9z 8 3x Y Z 8




Solve The Following System Of Linear Equation Graphically 2x 3y 17 0 And 4x Y 13 0 Shade The Region Brainly In




Solve The Following For X And Y By Using Method Of Elimination 2 X 3 Y 17 2 X 2 3 Y 1 5 Brainly In




Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples




Solving Linear Systems By Substitution



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



Http Www Wallace Ccfaculty Org Book 4 3 elimination Pdf




Chapter 3 Pairs Of Linear Equations In Two Variables Rd Sharma Solutions For Class 10 Mathematics Cbse Topperlearning




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt
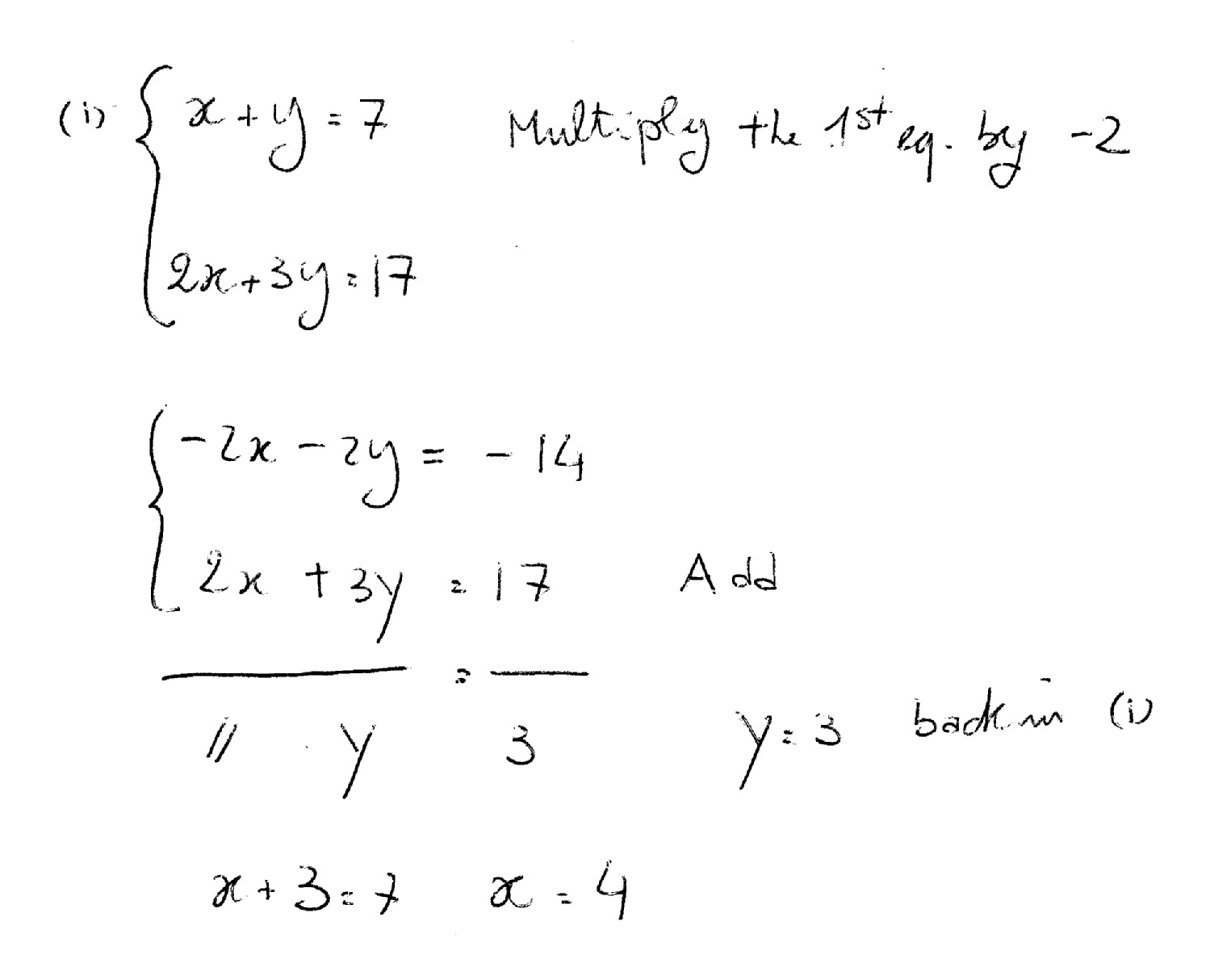



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic
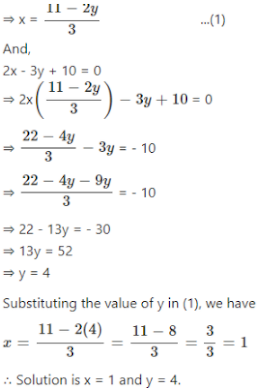



Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu




2 X 3 3 Y 5 0 5 X 1 4 Y 4 0 Solve It By Substitution Method Brainly In




2x 3y 17 3x 2y 6 Solve This Equation By Elimination Method Brainly In




Solve The Equations 4 2 X 1 9 3 Y 1 17 And 3 2 X 2 3 Y 6



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf




Chapter 3 Pairs Of Linear Equations In Two Variables Rd Sharma Solutions For Class 10 Mathematics Cbse Topperlearning




Blogjpmbahebyvn コンプリート 2 X 3 Y 17 2 X 2 3 Y 1 5 50
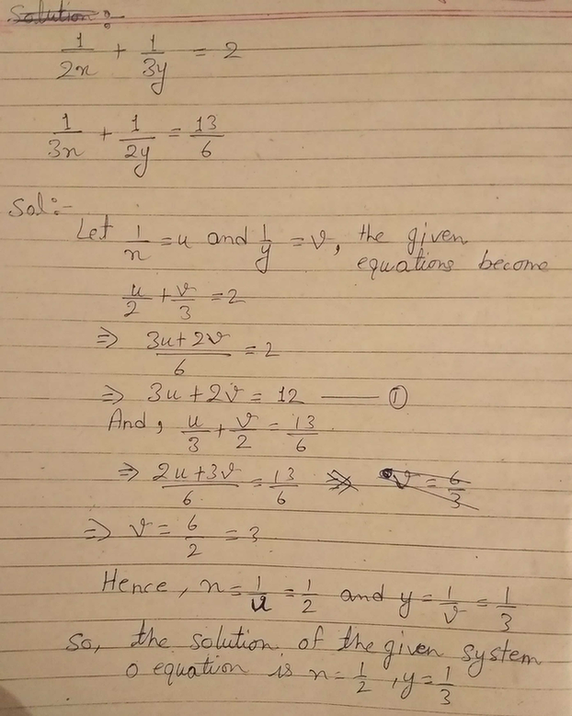



Exercise 3 5 1 Solve The Following Pairs Of Equations By Re Scholr




Step By Step Math Wolfram Alpha Blog




Pdf Advanced Engineering Mathematics Solutions Manual Ahmed Shaghasi Academia Edu
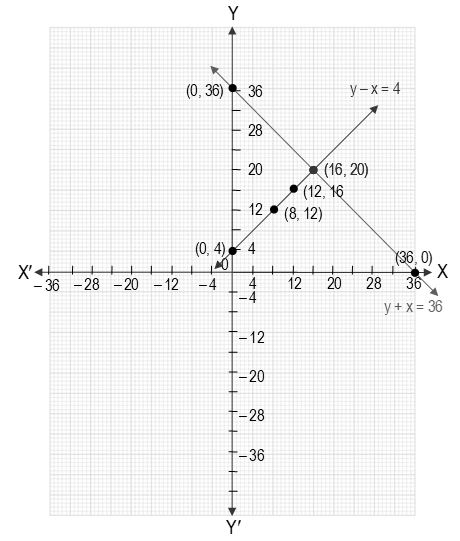



Pair Of Linear Equations In Two Variables




Solve Each Of The Following Systems Of Equations Using Matrix Method X Y 3 2x 3y 4z 17 Y 2z 7




Mathematics Notes
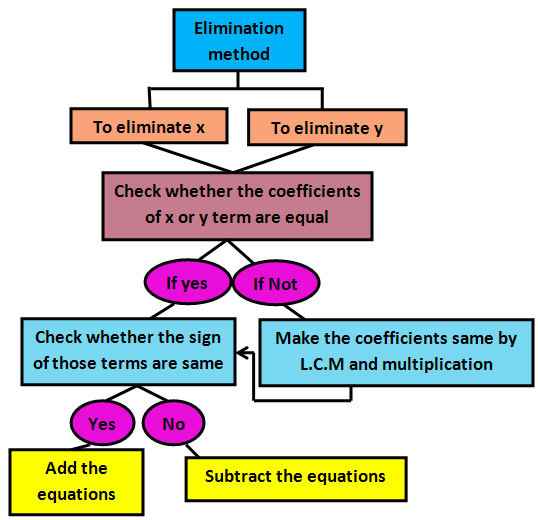



Elimination Method




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




5 X 3 Y 1 3 2x 2 3y 5 Brainly In



1



Systems Of Linear Equations



1




Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples




Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2




a Numer



Solve The Following Systems Of Equations 15 U 2 V 17 1 U 1 V 36 5 Sarthaks Econnect Largest Online Education Community




7x 3y 1 0




If 3x 5y 21 And 2x 3y 13 Then Find The Values Of X And Y



Onlinelibrary Wiley Com Doi Pdf 10 1002 Oth2




Chapter 6 Simultaneous Linear Equations Including Problems Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
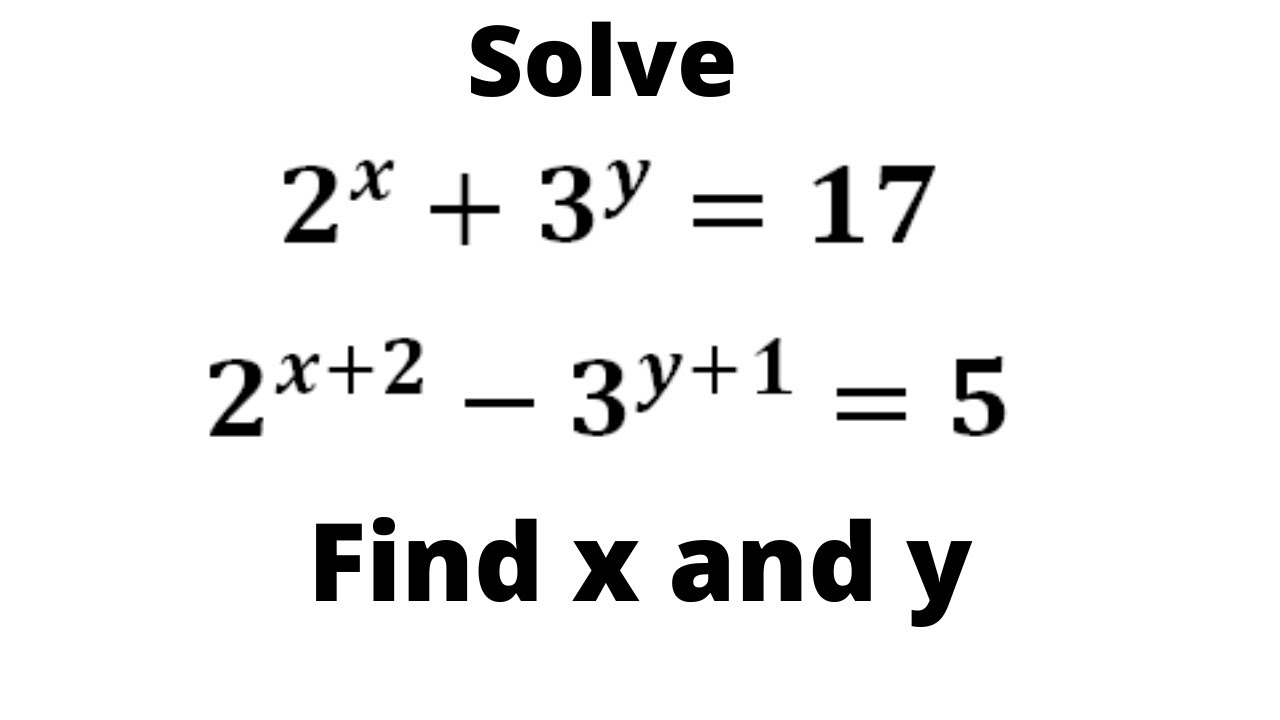



Solve 2 X 3 Y 17 2 X 2 3 Y 1 5 Find X And Y Youtube




Systems Of Equations With Substitution Y 5x 8 10x 2y 2 Video Khan Academy




Solve Each Of The Following System Of Equations By Elimination Method I X Y 8 2x 3y 1 Ii Maths Linear Equations In Two Variables Meritnation Com




Rs Aggarwal Solutions Class 10 Chapter 3 Linear Equations In Two Variables A Plus Topper



If X Y 3 X Y 1 Then What Is X Y Quora



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




If 2 X 3 Y 17 And 2 X 1 3 Y 1 5 Then What Is The Value Of X




2x 3 Y 3z 5 X 2y Z 4 3x Y 2z 3 Youtube



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu



Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Solving A System Of Equations Using A Matrix Precalculus Socratic
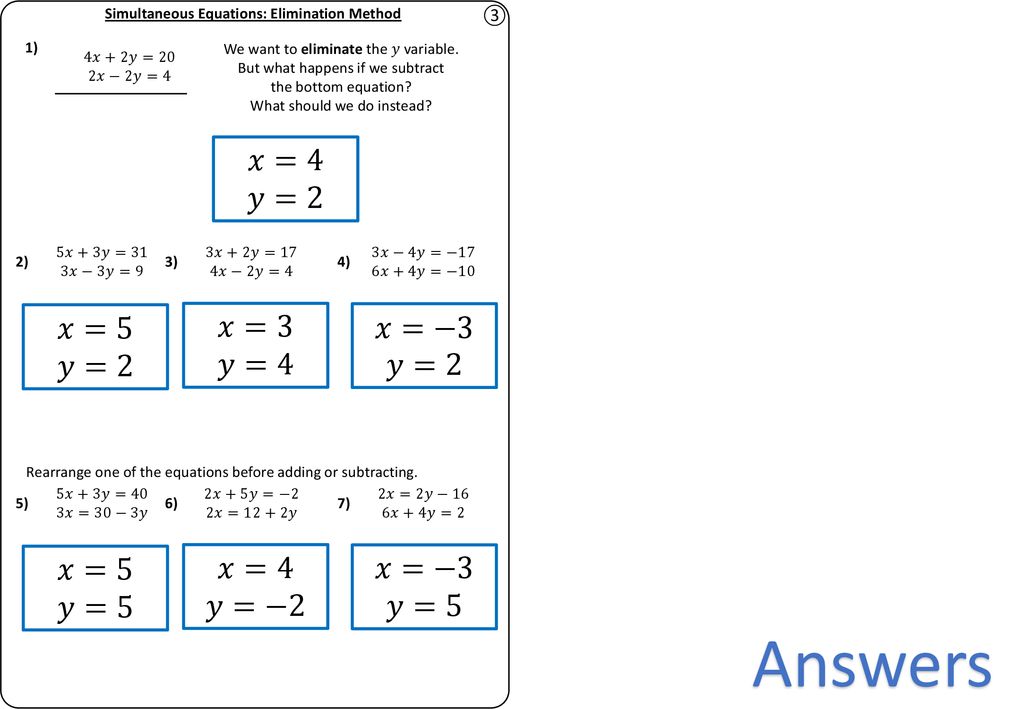



Simultaneous Equations Elimination Complete Lesson Ppt Download



2




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube




Solve This Q 2x 3y 172x 2 3y 1 5 Solve It By Elimination Or Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




Mca Unit 2 Computer Oriented Numerical Statistical Methods



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




Chapter 8 Problems



Solve The Following Systems Of Equations 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Sarthaks Econnect Largest Online Education Community




If 3x 2y 24 And 2x 3y 18 Then Find X Y And X Y




Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples




Solve System Of Linear Equations Using Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3 Mathematics Shaalaa Com




Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples




Answers



Using Gaussian Or Gauss Jordan Elimination X Y Z 5 2x 3y 6z 32 4x 5y 10z 8 Mathskey Com


